Time Value of Money (TVM) Calculations
TIME VALUE OF MONEY (TVM)
As a financial planner, you will need to perform various calculates to forecast the future based on past events. Most of these tasks require the use of a financial calculator or computer software program the calculations. To be successful, you must know the right formula to use before you can input data.
Key Variables
All TVM calculations involve solving for one of five key variables:
- N = The number of years of compounding periods
- I = The annual or periodic interest rate, discount rate or rate of return
- PV = The present value of the asset or liability
- PMT = The periodic payments required if any
- FV = The future value of the asset or liability
Rules when using a financial calculator
- Always clear the calculator before each operation (AC/ON, CE/C)
- Always use your calculator’s memory function to store interim calculations and set your calculator to display the maximum number of decimal places allowed; only round your final answer
- Start any TVM calculation by determining whether the first periodic payment starts at the beginning (BGN mode) or end (END mode) of the first period.
- End mode (END) is used for ordinary annuities, mortgages, and loans
- Begin mode (BGN) is used for annuities due, where cash flows start immediately.
- Enter TVM values for FV, PV and PMT as positive numbers for cash inflows and negative numbers for cash outflows, taken from the perspective of the client
- For example, the PV of a client’s mortgage is an inflow (they receive the money up front and pay it back over time – PMT is entered as a negative number)
- Enter data into the TVM functions in any order.
- Enter data for the I variable in percentage form, not decimal form. For example, enter 5 for 5%, not 0.05.
Facts to remember in TVM calculations
- As long as interest rates are positive, the FV of an amount is always greater than the PV
- Compounding more frequently than annually will always result in a higher future value than annual compounding at the same interest rate.
- The more frequent the compounding, the higher the future value
- All TVM calculations assume compound interest
- Fractional years can be handled by using decimals when entering the value for N.
- For example, making an investment for 18 months, can be entered as 1.5
- When the compounding period is one year, the effective annual rate is equal to the quoted annual rate. When compounding occurs more frequently than annually, the effective rate is always greater than the quoted annual rate.
- The future value of an annuity due will always be greater than the future value of a regular annuity
- The i in present value calculations is also referred to the discount rate, the required rate or the internal rate of return
The following equations may be helpful in answering questions that require calculations. Typically, these types of calculations are done using a financial calculator.
Future Value of a Single Amount
- Formula: FV = PV x (1 + i) ^ n

- More Frequent Compounding Periods:
- Interest may be compounded semi-annually, monthly, weekly, or
- For example, an interest rate of 8% compounded semi-annually will pay half the annual interest rate of 4% every 6 months
- Formula: FV = PV x (1 + i / f) ^ n x f
- i = the quoted annual interest rate
- f = the number of compounding periods in one year
- Referring back to our example above, and only changing the compounding period to semi-annually results in the following:
- FV = $5,000 x [1 + (0.085/2) ^ (3 x 2)
- FV = $5,000 x [1.0425] ^ 6
- FV = $5,000 x [1.2837
- FV = $6,418.39
Present Value of an Annuity
- As a financial planner, you may be asked to calculate how much a series of regular cash flows will be worth at some time in the future.
- For example, a client might ask what his portfolio will be worth at the end of five years if he contributes $15,000 per year for the next 5 years.
- In TVM calculations, an annuity is a series of level (amounts do not change from one payment to the next) cash flows over a specified period.
- Types:
- Regular annuity: known as an ordinary annuity, cash flows occur regularly at the end of each period.
- Annuity due: cash flows occur at the beginning of each period.
- Deferred annuity: cash flows begin beyond the first period.

- Note: when questions refer to contributions starting ‘today’, you must always set MODE to BGN
Present Value of a Single Amount
Formula: PV = FV / [(1 + I) ^ n]

- More Frequent Compounding Periods:
- As with future values, TVM problems can handle fractional years and multiple compounding periods when calculating present values

Present Value of an Annuity
- Financial planners will frequently encounter problems that require calculating the PV of a series of cash flows.
- For example, sometimes there is a need to calculate the amount needed to finance a client’s retirement of a child’s university education over a given number of years

Sometimes TVM calculations are more complex

Solving for the Number of Periods
Financial planners will sometimes have to solve for the number of time periods (i.e. years) it will take to grow an amount to a specified future value.

Solve for the Interest Rate
Solve for the Payments

Mortgages
Mortgage calculations present a variation on the standard PV calculations displayed thus far. In Canada, mortgage payments are paid every month, but mortgage rates are compounded semi-annually. For this reason, the interest factor must be adjusted in calculations.

Formulas
| Present Value of a Single Payment, Compounded Each Period: | 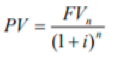 |
|---|---|
| Future Value of a Single Payment, Compounded Each Period: | |
| Present Value of a Stream of Payments: | 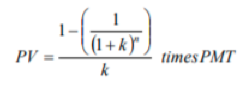 |
| Future Value of a Stream of Payments: | 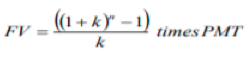 |
| Effective, Annual Rate | |
| Real Rate of Return | 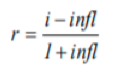 |
| Effect of Non-Annual Compounding | |
| Simple Interest (Return) Calculation: |
Variables
| FV | Future Value | i | Nominal, Annual Rate of Return |
|---|---|---|---|
| PV | Present Value | n | Number of Years |
| m | Number of Compounding periods per year | I t | Amount Returned or paid in year t |
| e | Effective, Annual Rate of Return | k | Periodic Rate of Return (i/m) |
| r | Real, Annual Rate of Return | infl | Annual Rate of Inflation |
| PMT | Payment |


